مجموعه زاویه های مثلث
دایره های طوسی
معمای مربع گمسده
تصاویر سه بعدی
اثبات قضییه فیثاغورس
قضییه تالس
عدد پی

مجموع زوایای داخلی مثلث
مجموع زوایای داخلی مثلث 180 درجه است

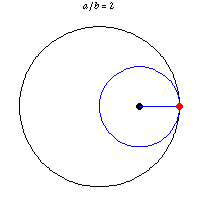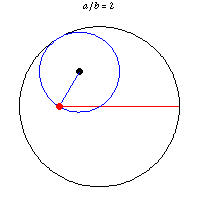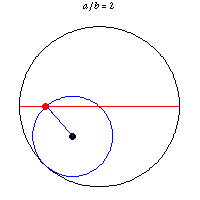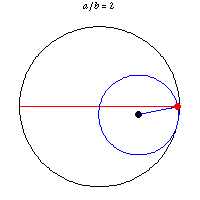
دایره های طوسی
تصویر زیر که به دایره های طوسی معروف است،چگونگی ترسیم یک خط راست با استفاده از دو دایره رانشان می دهد.
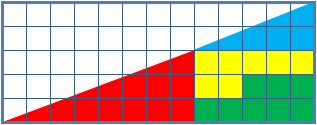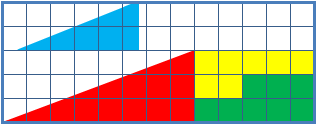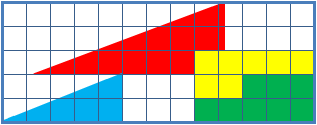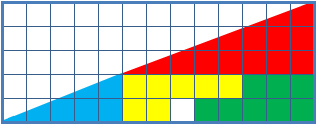
معمای مربع گم شده
این پازل دو ترکیب از اشکالی را نشان می دهد که ظاهراً هر دو یکمثلث قائم الزاویههستند. اما یکی از آنها یکمربع۱*۱فضای خالی دارد
انیمیشن اثبات قضيه ي فيثاغورث
اثبات بدون كلام :


دو حالت خاص :
ادامه مطلب
انیمیشنی برای عدد پی

دايره اي به شعاع 1 واحد در نظر بگيريد . همان طور كه در شكلزير مي بينيم مساحت چند ضلعي هاي منتظم محاط در اين دايره با افزايش تعداد ضلع ها به سمت مساحت دايره كه همانا عدد پي مي باشد ، نزديك و نزديك تر مي شوند

حلقه ی موبیوس همراه با تصویر متحرک

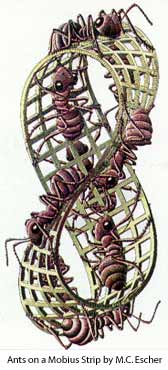

حـلقـه مـوبـيوس
مـنجـم آلـمانی <<مـوبـيوس>>يك شكل عـجيب كشف كرد كه بعدها به نام خود وی مشهور شد. موبيوس در مقاله ای به تشريح شكل شگفـت آوری پـرداخت و آن را نـوار<<يـك رويـه>>ناميد. معمـولاً انتـظار ما ايـن است كه هـر سـطحی دارای دو رويـه باشد. برای نمونه، يك ورق كاغـذ يك پـشت ويـك رو دارد. مـوبـيوس اقدام به ساخـتن نـواری يـك رويـه كـرد، كه امـكان تـشخيص پشت و رو، برای آن ممكن نيست. برای ساختن نوار موبيوس بايد دو سر يك نـوار مستطيل شكـل را<<پس ازدادن يك نـيم تاب به يكی از لـبه ها>>بهم بچسبانيد.اگر ازيك نقطه حلقه شروع به رنگ آميزی كنيم ومرتـباً جلو برويم، به زودی خواهـيم ديد كـه تـمامی سـطح نـوار رنگ آميزی شده است. ديگر خاصيت حلقه موبيوس آن است كه اگر نـوار را در امتداد طـول بـرش دهـيم، يك عـدد حلقه پيچ دار دورويهبه دست می آید.
در تصاویر بالاسه نمونه از نوار موبیوس را می بینید که تصویر دوم کار هـنرمند هـلندی <<اشه>>که درسال 1963بر روی چوب کنده کاری شده است. |
منبع : کتاب بازی های ریاضی و منطقی (آگوستینی)


